1.6. MEETRIKA TASASES AEG-RUUMIS

Meetrika on eeskiri, mille järgi arvutatakse kaugusi kahe ruumipunkti (aeg-ruumi punkti) vahel. Kui meetrika on antud, siis saab lisaks kaugustele arvutada ka geomeetriliste kujundite pindalasid ja ruumalasid. Rõhutagem, et füüsikaline (mõõdetav) kaugus kahe ruumipunkti vahel ei tohi sõltuda sellest, millise koordinaatsüsteemi me valime punktide asukoha kirjeldamiseks.

Tasases kolmruumis on meetrikat kõige lihtsam kirjeldada ristkoordinaadistikus. Kahe lõpmata lähedase punkti vaheline kaugus ruumis dl  avaldub järgmiselt:

(1.18)

kus dx, dy ja dz on vaadeldavate punktide vastavate koordinaatide vahed. Kuna kaugus kahe punkti vahel ei sõltu koordinaatsüsteemi valikust, siis teades, kuidas koordinaadid mingis teises koordinaatsüsteemis on seotud ristkoordinaadistikuga, on valemist (1.18) võimalik tuletada  avaldis selles uues koordinaatsüsteemis.

Näitena vaatleme lähemalt sfäärilisi koordinaate (vt joonis 6). Sfäärilised koordinaadid  ja  on seotud ristkoordinaatidega järgmiselt:

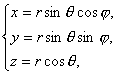(1.19)

kus  ja .

Arvutades valemist (1.19) diferentsiaalid dx, dy ja dz  ning asendades nad seejärel avaldisse (1.18), saamegi meetrika sfäärilistes koordinaatides:

.

(1.20)

Illustreerime meetrika (1.20) kasutamist mõningate näidetega joonise 6 baasil.

Võtame ühe punktidest (punkt O) sfääriliste koordinaatide alguspunktiks (vt joonis 6). Kaugus punktide O  ja A vahel on neid ühendava radiaalse sirglõigu pikkus. Selle sirge võrrandiks sfäärilistes koordinaatides on:

Järelikult :   ja . Integreerides viimast võrdust, saame punktide A ja O vaheliseks kauguseks punktide A  radiaalkoordinaadi r.

Kaugus kahe punkti vahel sfääri pinnal (kahe mõõtmeline kõverruum)

Kaugus kahe punkti vahel kõveras ruumis on neid punkte ühendava kõige lühema kõvera pikkus. Sfäärilisel pinnal on selliseks kõveraks suurringi kaar. Punkte P ja A (vt joonis 6) ühendava suurringi võrrandiks on: , . Seega ,  ja

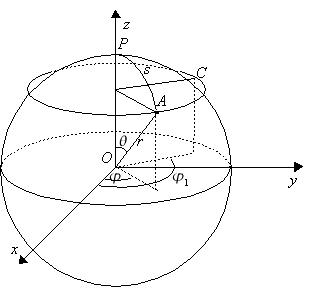
Joonis 6. Sfäärilised koordinaadid.

Koordinaatide alguspunkt on sfääritsentris O. Punkti A  koordinaatideks on:  ja

Integreerides viimast võrdust üle punktide P  ja A  ühendava kaare s, saame nende vaheliseks kauguseks , kus  on punkti A koordinaat. Meie poolt kerapinnal kasutatav koordinaadistik ühtib põhimõtteliselt geograafilise koordinaadistikuga: koordinaatjooned  kujutavad endast meridiaane ja koordinaatjooned  paralleele.

Vaatleme, kuidas leida kahe punkti C  ja A  vahelist kaugust mööda paralleeli. Sellisel juhul on ,  ja  (vt valemit (1.20) ja joonist 6). Järelikult peale integreerimist saame .

Nii nagu ristkoordinaatide korral on ka sfääriliste koordinaatide puhul pindala elemendiks infinitesimaalselt väikese (lõpmatult väikese) ristküliku pindala:

.

Asendades eelnevalt leitud  ja  avaldised ülal toodud võrdusesse, saame:

.

(1.21)

Lõpliku mõõdetega pinnatüki pindala leidmisel tuleb see jagada infinitesimaalselt väikesteks tükkideks ja seejärel nende tükikeste pindalad liita (integreerida). Valemi (1.21) kasutamisel tuleb siiski jälgida, et sfääriliste koordinaatide alguspunkt ei asuks mõõdetaval pinnal.

Ruumala elemendil on sfäärilistes koordinaatides järgmine kuju:

.

(1.22)

See on infinidesimaalselt väikese risttahuka ruumala.

Tasase aeg-ruumi meetrika (Minkowski meetrika)

Tegelikkuses asetleidvate, mistahes nähtuste kirjeldamisel ja uurimisel, tuleb objekti alati vaadelda nii ruumis kui ka ajas. Füüsikaline maailm on sündmuste maailm, st selle maailma punktideks on erinevad sündmused. Iga elementaarsündmus on iseloomustatud nelja koordinaadiga - kolm ruumikoordinaati (asukoht) ja üks ajakoordinaat (t). Nii on füüsikalises mõttes ruum ja aeg alati lahutamatud. Tegemist on ühtse tervikuga – aeg-ruumiga.

Kahe lähedase sündmuse vahelist kaugust ds tasases aeg-ruumis kirjeldab Minkowski meetrika:

,

(1.23)

kus c - on valguse kiirus, dt - sündmuste toimumise hetkede erinevus ja - sündmuste vastavate ruumikoordinaatide vahed. Füüsikaalases kirjanduses nimetatakse sündmuste vahelisi kauguse ruutu  tihti ka sündmuste vahelise intervalli ruuduks. Edaspidi on mugav kasutada sündmuste koordinaatide jaoks järgmisi tähistusi:

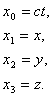(1.24)

Neis tähistustes omab meetrika (1.23) kuju:

(1.25)

ERT kohaselt on kõik inertsiaalsed taustsüsteemid võrdväärsed. Seega kahe sündmuse vahelise intervalli ruut (aeg-ruumi meetrika) ei sõltu inertsiaalsüsteemi valikust. Minkowski meetrikal on rida omadusi, mis erinevad kvalitatiivselt tasase kolmruumi meetrika omadustest. Näiteks, kuna footon liigub valguse kiirusega, siis tema jaoks on kõik footoniga toimuvad sündmused aeg-ruumis kaugusel null:  Nii nagu tasases (eukleidilises) kolmruumis, nii ka tasases aeg-ruumis on alati võimalik kasutada koordinaate, millel on vahetu meetriline mõte.