Помогает ли математика выиграть в лотерею?
В 2011 году жители испанской деревни Гранен выиграли в рождественскую лотерею «Большой куш» 720 миллионов евро. Как же им это удалось? Наверное они неплохо знали математику.
Любой человек, покупающий лотерейный билет, желает выиграть. Теоретически вероятность выпадения любых номеров строго равномерна. Исходя из этого, для расчета вероятности выигрыша в лотерею нужно просто посчитать количество комбинаций. Это и будет математическим обоснованием для лотереи.
Расчеты на примере 6 из 49
В лотерее 6/49 выпадает 6 шаров из 49 возможных и если 6 номеров в билете совпало, то вы - джек-потник. И неважно, в каком порядке выпали номерки. Вероятность такого события равна 1 из 13,983,816 (один из почти 14ти миллионов).
Этот крохотный шанс можно продемонстрировать следующим образом:
Начинаем с 49ти шаров в лототроне, каждый с уникальным номером, таким образом понятно, что вероятность угадать первый шар равна 1 из 49. Когда приходит время второго шара, в лототроне уже остается 48 шаров, таким образом, шансы угадать второй номерок становятся 1 из 48.
Таким образом, для для каждого варианта выбирания первого шара (который равен 1 из 49), есть только 48 вариантов выбора второго шара. Это означает, что шансы угадать 2 первых шара равны 1 из 49 × 48. Для вытаскивания третьего шара у нас остается уже всего 47 оставшихся шариков; соответственно, шансы угадать 3 первых номера составляют 1 из 49 × 48 × 47. Таким образом можно продолжить и дойти до шести шаров, в итоге получим шансы 1 из 49 × 48 × 47 × 46 × 45 × 44, что можно в виде формулы записать как 49!/ (49-6)!, где число
n!= n*(n-1)*(n-2)*(n-3)..*1
называется факториалом числа n. Перемножив получаем 10,068,347,520 (10 милиардов), что будет гораздо больше обещанных ранее 14 миллионов.
Чтобы разобраться в этом, нужно понять, что порядок выборки 6 номеров совершенно неважен. Т.е. если в билетике есть номера 1, 2, 3, 4, 5, и 6, он выигрышный, независимо от того, в каком порядке выпали все эти 6 номеров. В соотвествии с этим, любой набор из 6ти номеров, можно представить ввиде факториала 6 × 5 × 4 × 3 × 2 × 1 = 6! или 720 всевозможных комбинаций из одних и тех же 6ти номеров. Т.е. нам нужно поделить наши полученные 10 мильярдов на эти 720 вариантов, т.е. 10,068,347,520 делим на 720 и получаем 13,983,816, что может быть записано в виде формулы 49! / (6! × (49 - 6)!), или по-правильному:
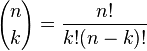
Эта функция называется комбинационной функцией; в Microsoft Excel даже есть она, под именем COMBIN(n, k). Например, COMBIN(49, 6) вернет 13,983,816. "Комбинация" означает группу выбранных номеров, независимо от порядка их выпада.
Математическое ожидание выигрыша
Расчет математического ожидания – это отличный способ определения того, является ли ставка прибыльной. Один математик даже использовал математическое ожидание для неоднократного выигрыша джек-пота лотереи.
Эта техника помогает игрокам определить ожидаемую сумму выигрыша или проигрыша по конкретной ставке, при этом положительное математическое ожидание означает, что предложение является выгодным. В качестве примера возьмем национальную лотерею Великобритании: в ней отрицательное математическое ожидание в -0,50 означает, что теоретически игроки теряют 50 пенсов на каждом поставленном фунте стерлингов, то есть ставка с таким математическим ожиданием является невыгодной.
Формула расчета математического ожидания при проведении лотереи довольно проста. Умножьте вероятность выигрыша на сумму, которую можно выиграть по ставке, и вычтите вероятность проигрыша, умноженную на сумму, которую можно проиграть:
(сумма выигрыша по ставке x вероятность выигрыша) – (сумма проигрыша по ставке x вероятность проигрыша)
Тем не менее, существует и определенная особенность при подсчете математического ожидания для лотерей. Она заключается в том, что если в каком-либо розыгрыше джек-пот не был выигран, его сумма добавляется к джек-поту следующего розыгрыша. Таким образом сумма джек-пота аккумулируется и в определенной момент может достигнуть значения, при котором математическое ожидание станет уже положительным.
Можно с уверенностью сказать, что среднестатистический игрок никогда не станет покупать 14 миллионов лотерейных билетов, но существуют стратегия, при которой можно воспользоваться преимуществами положительного математического ожидания – это так называемые лотерейные синдикаты (pools). Здесь все просто – вы объединяетесь с другими игроками, заранее договариваясь о распределении выигрыша. Таким образом, вы повышаете шансы на выигрыш, но его сумма будет меньше. Примером такого подхода был случай, когда жители испанской деревни Гранен в провинции Уэска в 2011 году объединились и выиграли лотерейный приз Большой куш. Каждый житель, заплативший около 20 евро за билет, получил около 400 тысяч евро. Всего деньги поделили между собой 1800 испанцев.
Изучить основы теории вероятности и статистики, необходимые для анализа лотерей и выработки выигрышной стратегии вы можете в Таллинском университете на учебной программе бакалавриата «Математика, экономическая математика и анализ данных». Подробнее об этой программе можно прочитать на странице Таллинского университета.
Успешной игры в лотерею!